Vamos ver na pratica como funciona essa regra:
Partindo da matriz 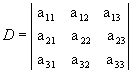
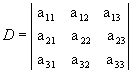
1º) Para começarmos devemos repetir as duas primeiras colunas ao lado da terceira, assim:
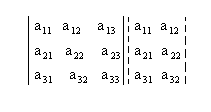
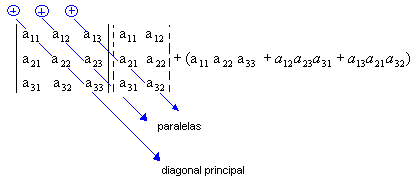
2º) Como será melhor exemplificado abaixo, agora devemos encontrar a soma dos produtos da diagonal principal com os dois produtos obtidos pela multiplicação das duas diagonais paralelas a essa diagonal, veja:
3º) Agora devemos encontrar a soma dos produtos da diagonal secundária com os dois produtos obtidos pela multiplicação das duas diagonais paralelas a essa diagonal, só que nesse caso a soma deve ser precedida de sinal negativo, isto é, devemos trocar os sinais dos valores que encontrarmos, desta maneira:

Desta forma:

Se aplicarmos Laplace e o resolvermos depois também encontraremos o mesmo resultado.
Fonte: http://www.somatematica.com.br/emedio/determinantes/determinantes3.php
Nenhum comentário:
Postar um comentário