Operações com matrizes: Multiplicação de matrizes

Multiplicação de matrizes é a mais complexa das operações com matrizes.
Nela não podemos apenas multiplicar os elementos respectivos, da mesma maneira que somamos ou subtraímos.
Desta maneira, o produto entre as matrizes A = ( a_ij) _{m x p}  e B = ( b_ij) _{p x n} é a matriz C = (c_ij) _{m x n} em que cada elemento c_ij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.
Aqui está um exemplo pra melhor ilustrar. Vamos multiplicar a matriz 
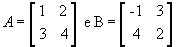
para podermos entender como obtermos cada c_ij.

• 1ª linha e 1ª coluna

   

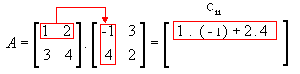
• 1ª linha e 2ª coluna

   

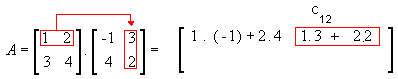
• 2ª linha e 1ª coluna

   

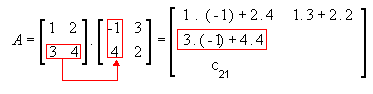
• 2ª linha e 2ª coluna

   

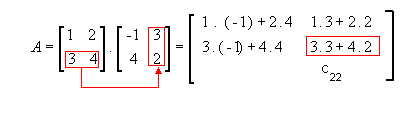
   Assim, .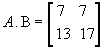

   Observe que:

 

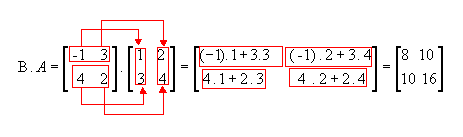
   Portanto, A.B é diferente de B.A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.

   Vejamos outro exemplo com as matrizes :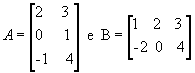

   

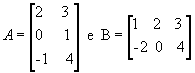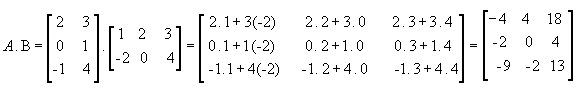
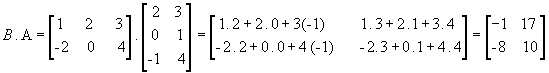
    Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número de linhas de B:

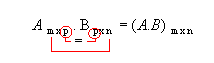
     A matriz produto terá o número de linhas de A (m) e o número de colunas de B(n):

• Se A_{3 x 2} e B _{2 x 5} , então ( A . B ) _{3 x 5}
• Se A _{4 x 1} e B _{2 x 3}, então não existe o produto
• Se A _{4 x 2} e B _{2 x 1}, então ( A . B ) _{4 x 1}

Propriedades:

Associativa: (A.B).C = A.B.C

Distributiva: (A+B).C = A.C+B.C e A . ( B + C ) = A . B + A . C 

Fonte: http://www.somatematica.com.br/emedio/matrizes/matrizes4.php , dia 06/03/2014 ás 18:04