Mais alguns tipos de matrizes

 Numa matriz quadrada definimos a diagonal principal e a diagonal secundária. A principal é formada pelos elementos a_ij tais que i = j. Na secundária, temos i + j = n + 1.

    Veja:

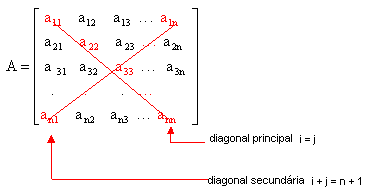
Observe a matriz a seguir:

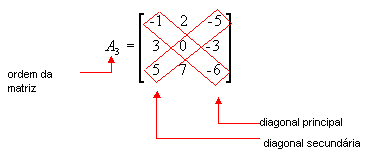
Matriz diagonal: é uma matriz quadrada em que os elementos que não estão na diagonal principal são nulos, ou seja, são zeros.
Exemplo:


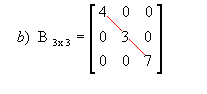
Matriz Identidade

Uma matriz identidade é uma matriz quadrada onde na sua diagonal principal os elementos tem valor 1 e os demais possuem valor zero.
Exemplo: I_n, onde n representa a ordem da matriz identidade.
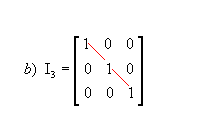matriz identidade de terceira ordem.

Portanto podemos defini-la da seguinte forma:


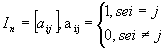
Matriz transposta:
Se uma matriz A é de ordem mxn uma matriz transposta, representada por A^t é uma matriz do tipo nxm, ou seja trocamos ordenadamente a linha pela coluna, e vice e versa.
Exemplo:

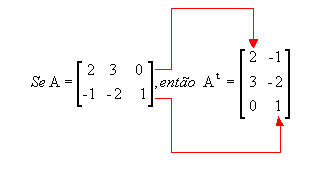
Note que a 1ª linha de A corresponde à 1ª coluna de A^t e a 2ª linha de A corresponde à 2ª coluna de A^t.

Matriz simétrica: matriz quadrada onde A = A^t .

Exemplo: 
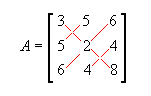se olharmos com atenção iremos perceber que a 1ª linha é igual a 1ª coluna, e assim por diante.

Matriz oposta: é a matriz -A, onde trocamos todos os sinais de A para obtê-la.
Exemplo:



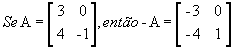
Fonte: http://www.somatematica.com.br/emedio/matrizes/matrizes2.php dia 02/03/2014 as 12:31