Você gosta de aulas por vídeo?
Nesse link do youtube https://www.youtube.com/watch?v=sw18GQESKpA você terá
acesso ao primeiro de uma serie de vídeos sobre matrizes e determinantes.
Assista aos vídeos e compreenda um pouco melhor esse mundo de matrizes e
determinantes.
Matrizes e Determinantes aqui serão explicadas de maneira clara e de facil compreensão, além de exercicíos e desafios para uma melhor compreensão.
domingo, 6 de abril de 2014
domingo, 9 de março de 2014
Para treinar determinante
1) Unicap - PE
.jpg)


.jpg)

Fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-determinantes.htm#resposta-1076
Calcule o valor de x, a fim de que o determinante da matriz A seja nulo.


Resposta
.jpg)

2) Determine o valor de x para que o determinante da matriz A seja igual a 8.

Resposta
.jpg)
nesse caso possuímos dois valores válidos pra x
Portanto :

Fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-determinantes.htm#resposta-1076
Propriedades dos determinantes
Nesse link http://www.somatematica.com.br/emedio/determinantes/determinantes4.php , você encontrará propriedades que facilitam o desenvolvimento do determinante em certos casos. Espero que sejam úteis,
E para matriz de ordem superior a 3?
Para as matrizes de ordem superior a 3 devemos aplicar o Teorema de Laplace até obtermos determinantes de ordem 3 e então usamos a Regra de Sarrus.
Regra de Sarrus
Para calcularmos o determinante de uma matriz de ordem 3 existe um método que veremos agora. É a REGRA DE SARRUS. O matemático Pierre Frédéric Sarrus (1789-1861), nascido em Saint-Affrique foi o criador dessa regra.
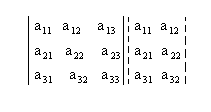


Vamos ver na pratica como funciona essa regra:
Partindo da matriz 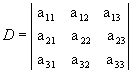
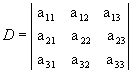
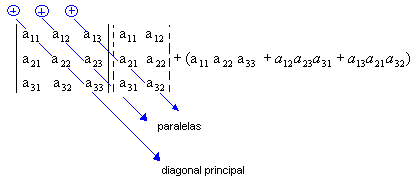
1º) Para começarmos devemos repetir as duas primeiras colunas ao lado da terceira, assim:
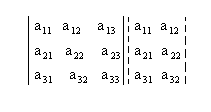
2º) Como será melhor exemplificado abaixo, agora devemos encontrar a soma dos produtos da diagonal principal com os dois produtos obtidos pela multiplicação das duas diagonais paralelas a essa diagonal, veja:

3º) Agora devemos encontrar a soma dos produtos da diagonal secundária com os dois produtos obtidos pela multiplicação das duas diagonais paralelas a essa diagonal, só que nesse caso a soma deve ser precedida de sinal negativo, isto é, devemos trocar os sinais dos valores que encontrarmos, desta maneira:

Desta forma:

Se aplicarmos Laplace e o resolvermos depois também encontraremos o mesmo resultado.
Fonte: http://www.somatematica.com.br/emedio/determinantes/determinantes3.php
Teorema de LAPLACE
O teorema de Laplace consiste em escolher uma das filas (linha ou coluna) da matriz e somar os produtos dos elementos dessa fila pelos seus respectivos cofatores.
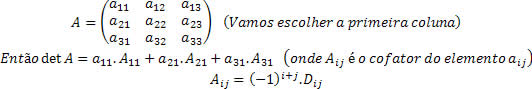
Dica: sempre escolha a linha ou coluna que tenha mais zeros, pois isso facilita e muito os cálculos.
Fonte: http://www.brasilescola.com/matematica/teorema-laplace.htm
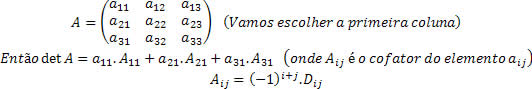
Dica: sempre escolha a linha ou coluna que tenha mais zeros, pois isso facilita e muito os cálculos.
Fonte: http://www.brasilescola.com/matematica/teorema-laplace.htm
Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Veja:
a) Dada  , os cofatores relativos aos elementos a11 e a12 da matriz M são:
, os cofatores relativos aos elementos a11 e a12 da matriz M são:
 , os cofatores relativos aos elementos a11 e a12 da matriz M são:
, os cofatores relativos aos elementos a11 e a12 da matriz M são: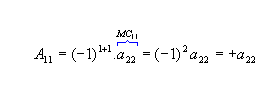 | 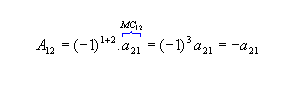 |
b) Sendo  , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31:
 , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31: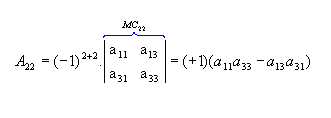 |
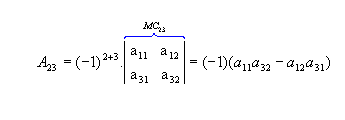 |
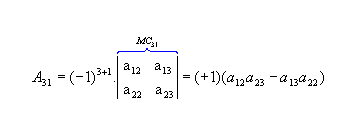 |
MENOR COMPLEMENTAR
O menor complementar é um elemento aij de uma matriz M, quadrada e de ordem n>1, o determinante MCij , de ordem n - 1, associado à matriz obtida de M quando suprimimos a linha e a coluna que passam por aij.
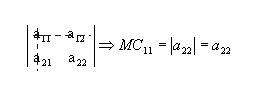
Olhe o seguinte exemplo:
Para calcularmos essa matriz  e determinarmos o menor complementar relativo ao elemento a11(MC11), primeiro retiramos a linha 1 e a coluna 1
e determinarmos o menor complementar relativo ao elemento a11(MC11), primeiro retiramos a linha 1 e a coluna 1
 e determinarmos o menor complementar relativo ao elemento a11(MC11), primeiro retiramos a linha 1 e a coluna 1
e determinarmos o menor complementar relativo ao elemento a11(MC11), primeiro retiramos a linha 1 e a coluna 1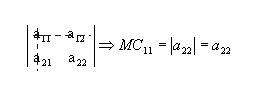
E se ao invés de uma matriz quadrada de ordem 2 tivéssemos uma de ordem 3?
Procederíamos da mesma forma veja:
Matriz com a qual trabalharemos é 

Para 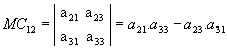
Fonte:http://www.somatematica.com.br/emedio/determinantes/determinantes2.php
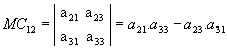
Fonte:http://www.somatematica.com.br/emedio/determinantes/determinantes2.php
Então como calculamos o determinante de uma matriz?
Vamos começar pela matriz quadrada de 1ª ordem, nesse caso temos M=[a11], o seu determinante é o número real a11: det M =Ia11I = a11
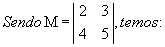
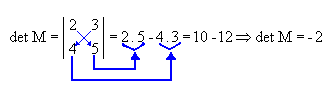
Podemos dizer então que numa matriz de 1ª ordem o próprio elemento é o seu determinante.
Atenção: podemos representar o determinante entre duas barras verticais, que no caso nada tem a ver com módulo, isto é, se o número é negativo, ele permanecerá negativo.
Agora vejamos para uma matriz de 2ª ordem:
tendo a matriz  o seu determinante é
o seu determinante é 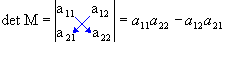
 o seu determinante é
o seu determinante é 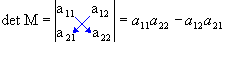
Nesse caso, temos que o determinante é o resultado da diferença do produto da diagonal principal pelo produto da diagonal secundaria.
Vamos entender melhor analisando o seguinte exemplo:
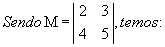
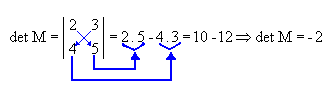
Fonte: http://www.somatematica.com.br/emedio/determinantes/determinantes.php
Utilidade prática do Determinante
Determinante nos é muito útil
- na resolução de alguns tipos de sistemas de equações lineares;
-no cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices
Fonte: http://www.somatematica.com.br/emedio/determinantes/determinantes.php
- na resolução de alguns tipos de sistemas de equações lineares;
-no cálculo da área de um triângulo situado no plano cartesiano, quando são conhecidas as coordenadas dos seus vértices
Fonte: http://www.somatematica.com.br/emedio/determinantes/determinantes.php
DETERMINANTES
O que é determinante?
Determinante é um número relacionado a uma matriz quadrada de ordem n. O determinante de uma matziz A, é representado por det A, é o número obtido quando se opera com os elementos dessa matriz
Determinante é um número relacionado a uma matriz quadrada de ordem n. O determinante de uma matziz A, é representado por det A, é o número obtido quando se opera com os elementos dessa matriz
Mais alguns exercícios, desafio para treinar
1) (PUC-GO) Analise a afirmação seguinte: Se A é uma matriz quadrada, então A + AT é uma matriz simétrica e A – AT é uma matriz antissimétrica.
Resposta

Afirmação verdadeira
2) Resolva a equação 2Xt – 3A = B, se A = e B =
e B = 
Resposta

3)
.jpg)
Resposta
Como já vimos anteriormente, a multiplicação de uma matriz pela sua inversa deverá nos dar uma matriz identidade, portanto
.jpg)
a Matriz B é inversa da Matriz A.
4) UFSC
Resposta

Afirmação verdadeira
2) Resolva a equação 2Xt – 3A = B, se A =
 e B =
e B = 
Resposta

3)
.jpg)
Resposta
Como já vimos anteriormente, a multiplicação de uma matriz pela sua inversa deverá nos dar uma matriz identidade, portanto
.jpg)
a Matriz B é inversa da Matriz A.
4) UFSC
Sejam A=(aij )4x3 e B=(bij )3x4 duas matrizes definidas por aij=i+j e bij=2i+j, respectivamente. Se A.B=C, então qual é o elemento c32 da matriz C?
Resposta
O elemento requerido é o da terceira linha e da segunda coluna, que é resultado de uma multiplicação de duas matrizes. Sabemos pela propriedade de multiplicação que este elemento é proveniente da multiplicação da terceira linha da matriz A pela segunda coluna da matriz B. Portanto, precisamos escrever apenas estes elementos.

GOSTOU DESSES EXERCÍCIOS? QUER MAIS ?
TODOS OS EXERCÍCIOS AQUI POSTADOS FORAM RETIRADOS DO SITE http://exercicios.brasilescola.com/matematica/ ACESSE E VEJA MAIS EXERCÍCIOS DE MATRIZES E DE DIVERSAS OUTRAS ÁREAS DE MATEMÁTICA E ATÉ MESMO OUTRAS ÁREAS DE ENSINO

GOSTOU DESSES EXERCÍCIOS? QUER MAIS ?
TODOS OS EXERCÍCIOS AQUI POSTADOS FORAM RETIRADOS DO SITE http://exercicios.brasilescola.com/matematica/ ACESSE E VEJA MAIS EXERCÍCIOS DE MATRIZES E DE DIVERSAS OUTRAS ÁREAS DE MATEMÁTICA E ATÉ MESMO OUTRAS ÁREAS DE ENSINO
Alguns exercícios de matriz com resposta
1) Determine a matriz C, resultado da soma das matrizes A e B.

Resposta

2) Determine a matriz resultante da subtração das seguintes matrizes:




Determine:
a) A + B – C
b) A – B – C
Resposta

4) Adicione as matrizes e determine os valores das incógnitas.


Resposta

2) Determine a matriz resultante da subtração das seguintes matrizes:

Resposta


3) Considerando as matrizes:

Determine:
a) A + B – C
b) A – B – C
Resposta

4) Adicione as matrizes e determine os valores das incógnitas.

Resposta
x + x = 10
2x = 10
x = 5
2x = 10
x = 5
y + 3 = – 1
y = – 1 – 3
y = – 4
y = – 1 – 3
y = – 4
3 + t = 4
t = 4 – 3
t = 1
t = 4 – 3
t = 1
2z + z = 18
3z = 18
z = 18/3
z = 6
Fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-adicao-subtracao-matrizes.htm#resposta-373
3z = 18
z = 18/3
z = 6
Fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-adicao-subtracao-matrizes.htm#resposta-373
Matriz inversa
Matriz inversa é a matriz que quando multiplicada pela matriz A deve obter como resultado uma matriz identidade. Note que para que essa afirmação seja valida a propriedade comutativa deve ser verdadeira nesse caso.
quinta-feira, 6 de março de 2014
Operações com matrizes: Multiplicação de matrizes
Multiplicação de matrizes é a mais complexa das operações com matrizes.
Nela não podemos apenas multiplicar os elementos respectivos, da mesma maneira que somamos ou subtraímos.
Desta maneira, o produto entre as matrizes A = ( aij) m x p e B = ( bij) p x n é a matriz C = (cij) m x n em que cada elemento cij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.
Aqui está um exemplo pra melhor ilustrar. Vamos multiplicar a matriz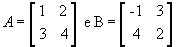
para podermos entender como obtermos cada cij.
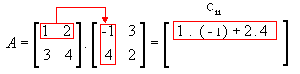
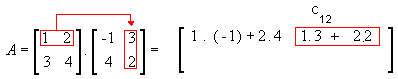
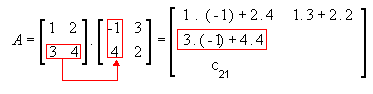
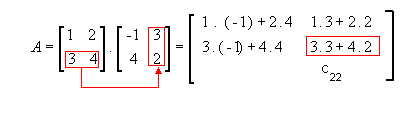
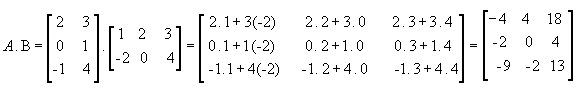
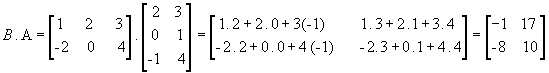
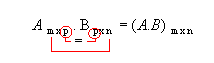
Nela não podemos apenas multiplicar os elementos respectivos, da mesma maneira que somamos ou subtraímos.
Desta maneira, o produto entre as matrizes A = ( aij) m x p e B = ( bij) p x n é a matriz C = (cij) m x n em que cada elemento cij é obtido por meio da soma dos produtos dos elementos correspondentes da i-ésima linha de A pelos elementos da j-ésima coluna B.
Aqui está um exemplo pra melhor ilustrar. Vamos multiplicar a matriz
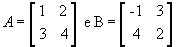
para podermos entender como obtermos cada cij.
- 1ª linha e 1ª coluna
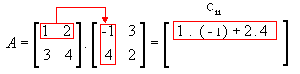
- 1ª linha e 2ª coluna
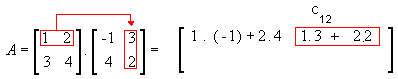
- 2ª linha e 1ª coluna
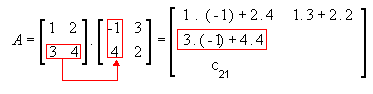
- 2ª linha e 2ª coluna
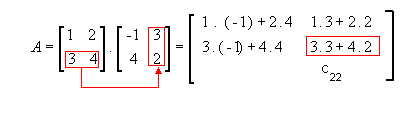
Assim, 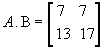 .
.
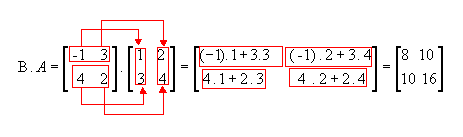
Observe que:

Portanto, A.B é diferente de B.A, ou seja, para a multiplicação de matrizes não vale a propriedade comutativa.
Vejamos outro exemplo com as matrizes 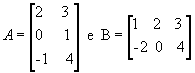 :
:
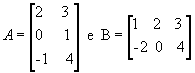 :
: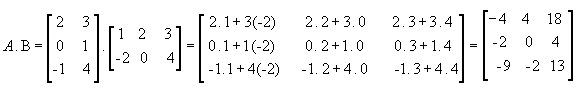
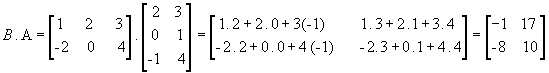
Da definição, temos que a matriz produto A . B só existe se o número de colunas de A for igual ao número de linhas de B:
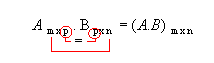
A matriz produto terá o número de linhas de A (m) e o número de colunas de B(n):
- Se A3 x 2 e B 2 x 5 , então ( A . B ) 3 x 5
- Se A 4 x 1 e B 2 x 3, então não existe o produto
- Se A 4 x 2 e B 2 x 1, então ( A . B ) 4 x 1
Propriedades:
Associativa: (A.B).C = A.B.C
Distributiva: (A+B).C = A.C+B.C e A . ( B + C ) = A . B + A . C
Fonte: http://www.somatematica.com.br/emedio/matrizes/matrizes4.php , dia 06/03/2014 ás 18:04
Assinar:
Postagens (Atom)