Você gosta de aulas por vídeo?
Nesse link do youtube https://www.youtube.com/watch?v=sw18GQESKpA você terá
acesso ao primeiro de uma serie de vídeos sobre matrizes e determinantes.
Assista aos vídeos e compreenda um pouco melhor esse mundo de matrizes e
determinantes.
Quarteto Fantástico & As Matrizes e Determinantes
Matrizes e Determinantes aqui serão explicadas de maneira clara e de facil compreensão, além de exercicíos e desafios para uma melhor compreensão.
domingo, 6 de abril de 2014
domingo, 9 de março de 2014
Para treinar determinante
1) Unicap - PE
.jpg)


.jpg)

Fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-determinantes.htm#resposta-1076
Calcule o valor de x, a fim de que o determinante da matriz A seja nulo.


Resposta
.jpg)

2) Determine o valor de x para que o determinante da matriz A seja igual a 8.

Resposta
.jpg)
nesse caso possuímos dois valores válidos pra x
Portanto :

Fonte: http://exercicios.brasilescola.com/matematica/exercicios-sobre-determinantes.htm#resposta-1076
Propriedades dos determinantes
Nesse link http://www.somatematica.com.br/emedio/determinantes/determinantes4.php , você encontrará propriedades que facilitam o desenvolvimento do determinante em certos casos. Espero que sejam úteis,
E para matriz de ordem superior a 3?
Para as matrizes de ordem superior a 3 devemos aplicar o Teorema de Laplace até obtermos determinantes de ordem 3 e então usamos a Regra de Sarrus.
Regra de Sarrus
Para calcularmos o determinante de uma matriz de ordem 3 existe um método que veremos agora. É a REGRA DE SARRUS. O matemático Pierre Frédéric Sarrus (1789-1861), nascido em Saint-Affrique foi o criador dessa regra.
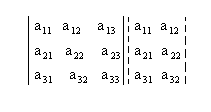


Vamos ver na pratica como funciona essa regra:
Partindo da matriz 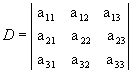
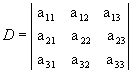
1º) Para começarmos devemos repetir as duas primeiras colunas ao lado da terceira, assim:
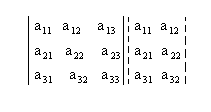
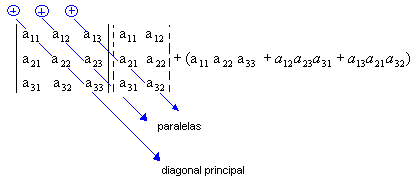
2º) Como será melhor exemplificado abaixo, agora devemos encontrar a soma dos produtos da diagonal principal com os dois produtos obtidos pela multiplicação das duas diagonais paralelas a essa diagonal, veja:

3º) Agora devemos encontrar a soma dos produtos da diagonal secundária com os dois produtos obtidos pela multiplicação das duas diagonais paralelas a essa diagonal, só que nesse caso a soma deve ser precedida de sinal negativo, isto é, devemos trocar os sinais dos valores que encontrarmos, desta maneira:

Desta forma:

Se aplicarmos Laplace e o resolvermos depois também encontraremos o mesmo resultado.
Fonte: http://www.somatematica.com.br/emedio/determinantes/determinantes3.php
Teorema de LAPLACE
O teorema de Laplace consiste em escolher uma das filas (linha ou coluna) da matriz e somar os produtos dos elementos dessa fila pelos seus respectivos cofatores.
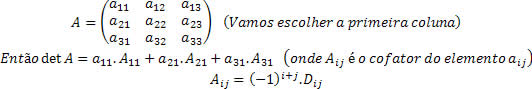
Dica: sempre escolha a linha ou coluna que tenha mais zeros, pois isso facilita e muito os cálculos.
Fonte: http://www.brasilescola.com/matematica/teorema-laplace.htm
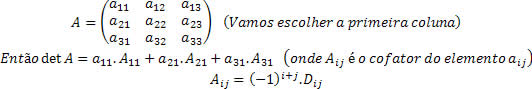
Dica: sempre escolha a linha ou coluna que tenha mais zeros, pois isso facilita e muito os cálculos.
Fonte: http://www.brasilescola.com/matematica/teorema-laplace.htm
Cofator
Chamamos de cofator ou complemento algébrico relativo a um elemento aij de uma matriz quadrada de ordem n o número Aij tal que Aij = (-1)i+j . MCij .
Veja:
a) Dada  , os cofatores relativos aos elementos a11 e a12 da matriz M são:
, os cofatores relativos aos elementos a11 e a12 da matriz M são:
 , os cofatores relativos aos elementos a11 e a12 da matriz M são:
, os cofatores relativos aos elementos a11 e a12 da matriz M são: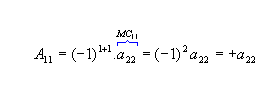 | 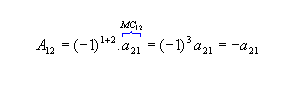 |
b) Sendo  , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31:
 , vamos calcular os cofatores A22, A23 e A31:
, vamos calcular os cofatores A22, A23 e A31: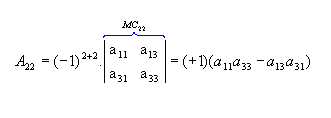 |
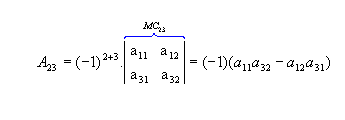 |
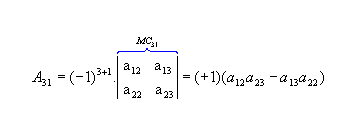 |
Assinar:
Postagens (Atom)